Calcul des forces 

Calcul d'un fuseau

Une fois que le volume souhaité est déterminé, il convient de déterminé le nombre de fuseau. Ce dernier sera calculé de manière à ce que la largeur L des fuseaux à l'équateur (en tenant compte de la surface de recouvrement) soit la plus proche possible de la largeur du tissu disponible.

Ce calcul a pour but de pour limiter le nombre de fuseau en veillant toutefois à ce que le nombre de fuseau ne soit pas trop faible pour éviter d'avoir un ballon « à facettes »

Appelons le nombre de fuseau déterminé n

Appelons R le rayon, connu lui aussi en fonction du volume choisi.

●         Méthode géométrique

Cette méthode empirique est applicable uniquement pour des fuseaux sphériques. A l'équateur, la largeur du fuseau sera donc :

 L = (2πR)/n = longueur de l'arc de cercle AB

La méthode consiste à tracer géométriquement le fuseau. Pour cela, tracer sur un plan deux droites perpendiculaires.

Le centre sera le centre du fuseau nommé O.

Sur la droite horizontale, tracer la longueur de l'arc de cercle AB qui est égale à L

Sur la droite verticale, tracer les points C et D représentant les pointes du fuseau.

OC = OD = la demi circonférence de la sphère = πR

Maintenant tracer un cercle de rayon L et ayant pour centre O. On obtient ceci :

On appellera M le point d'intersection entre la droite CD qui est l'axe de symétrie vertical du fuseau et le cercle.

Diviser maintenant l'arc de quadrant BM en un nombre m quelconques de parties égales

(les aéronautes de l'époque le divisait en 20 ce qui correspondait à un arc de cercle de 4,5°).

Tracer des droites perpendiculaires à AB passant par les points définis ci-dessus le long de l'arc BM

Exemple pour m = 5 :

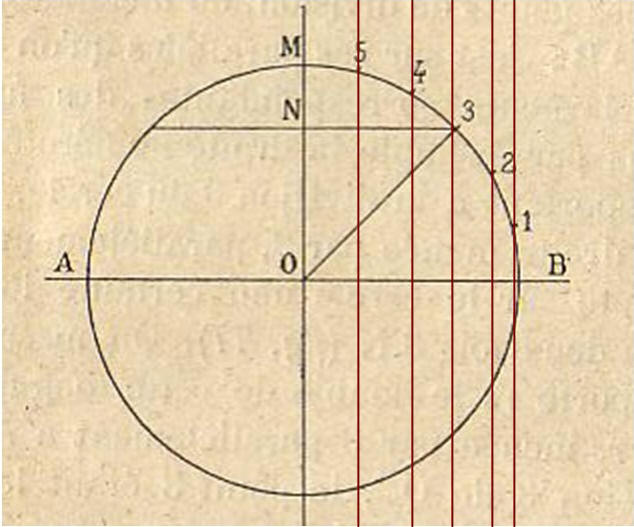
Diviser maintenant le segment OC et OD de ce même nombre m.

Tracer les droites parallèles à AB passant par les points définis ci-dessus le long de OD.

Exemple :

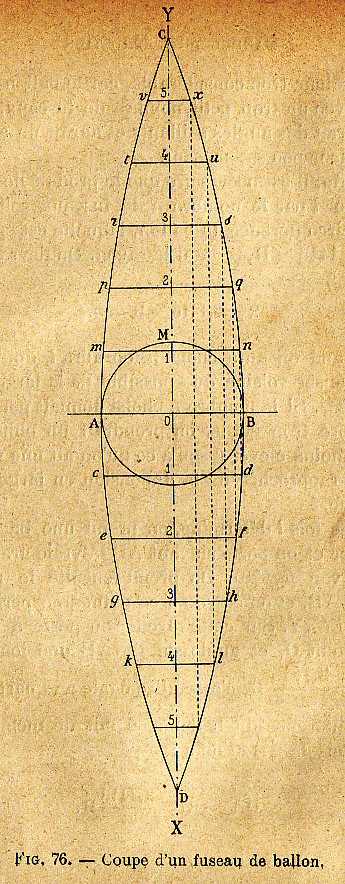
L'intersection des droites tracées ayant le même « numéro » correspond ainsi aux points représentant le bord du fuseau.

●         Méthode algébrique

Elle est beaucoup plus simple à mettre en oeuvre que la précédente avec les moyens informatiques d'aujourd'hui !

Considérons une sphère avec un nombre m de méridien (ou parallèle).

n étant toujours le nombre de fuseau déterminé à l'équateur et R le rayon de la sphère.

Nous savons qu'en tout point M de l'arc de cercle, la largeur L du fuseau est la longueur (ou circonférence) du méridien

divisé par le nombre de fuseau soit  L = (2πy)/n

Avec y = Rcosα et x =  Rsinα

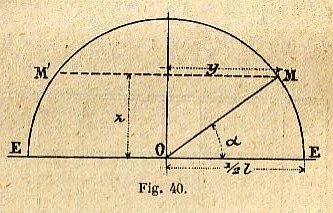
Ainsi pour chaque valeur de l'angle α, on connaît la valeur correspondante de x et de y et ainsi la largeur du fuseau.

Un tableur type Excel vous trace facilement le dessin d'un fuseau :

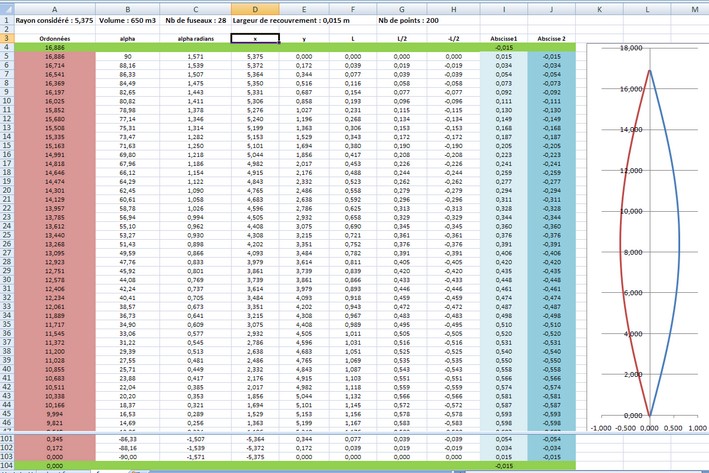
Fichier de calcul (comprenant la largeur de recouvrement pour le collage)

Calcul de l'appendice

L'appendice est un clapet de sureté : plus le ballon s'élève vite, plus le gaz qui se dilate doit trouver une issue pour éviter

toute surpression capable de faire éclater l'enveloppe.

Une des formule (G. Espitallier) permettant de calculer l'appendice avec l'hydrogène est la suivante :

l = 4.d et d = 0,008.D^3/2

avec l = longueur de l'appendice, d =diamètre de l'appendice et D= diamètre du ballon

Tout dépend de la pression interne que l'on souhaite. Pour un ballon captif qui doit être résistant aux rafales de vents, on va plutôt augmenter

sa longueur (voir plus haut la formule de la pression interne à un ballon ).

On lit dans les écrits que certains aéronautes ont supprimé la manche d'appendice pour la remplacer par une soupape avec

clapet monté sur ressort. Ce système fonctionnait très bien mais il fallait être sûr de son bon fonctionnement en permanence, le risque

étant très grand.